The goals of the course are to look at different ways to analyze algorithms, and use different "models" to think about algorithms.
Harvard COMPSCI 224:
- Fall 2014 Lectures (Jelani Nelson)
- Fall 2014 Website
MIT Advanced Algorithms (6.854):
- Fall 2013 Lectures (David Karger)
- Spring 2016 Lectures (Ankur Moitra)
- Spring 2016 Website
Static Predecessor (CS224, Lectures 1 & 2)
The Static Predecessor problem is a data structural problem, where a set S of items is to be queried pred(x) for the largest element z such that max{z, x ∈ S: z < x}. In the static predecessor problem, the set S is fixed (in contrast with a dynamic predecessor problem, which would include insert operations). One approach to this problem is to store the numbers sorted and do binary search, which would result in log(n) predecessor query. If the numbers were stored in a BST, insertion would also run in log(n).
In a comparison based model, sorting cannot be done better than n log(n). To do better than n log(n), we need a different model. One such model is the Word Ram model, in which operations are performed on words of size w. For a model with word size w, the universe U of values is {0, ..., 2 ^ (w - 1)}. We assume a pointer into the space (i.e. a memory address) fits into a word of size w. The word ram model supports standard arithmetic and bit-wise operations in constant time.
For the predecessor problem, we require at least O(n) space (since we have n items), and w is at least lg(n). Two different data structures for solving the problem get different bounds, and which is better or worse depends on the size of w relative to n:
- van Emde Boas Trees: support update and query in O(log w), O(U) space (can be made O(n) with randomization). y-fast tries get the same bounds.
- Fusion Trees: can be made dynamic (not covered), query in O(log n / log w)
If we know w, we can choose the better data structure, and get the minimum bound of the two. This works out to a bound of sqrt(lg n). This implies that with dynamic fusion trees, we can sort in time n * sqrt(lg n). Time bounds of O(n lg lg n) and O(n sqrt( lg lg n)) with linear space are possible, and it's an open question if O(n) is possible in the word ram model.
van Emde Boas Trees
I looked at vEB trees before, as part of my massive post on 6.046. vEB trees are a recursively defined data structure over a universe U that is addressible in a single word w. The vEB is an n-ary tree over this universe where n is the square root of U. Put another way, a vEB over positive 32 bit integers will consist of several components:
- an array of 2^16, 16 bit vEB children (or for better space efficiency, a hashmap)
- a single 16 bit "summary" vEB
- auxilary information such as min, max, size, etc.
When a number is inserted, it is broken down by successively dividing its bits. Say we insert 2 billion into our tree, which is represented in binary as 1110111001101011001010000000000. If we split the bits, we get 0111011100110101 (30517) and 1001010000000000 (37888). The top bits get inserted into the summary, and the bottom bits are inserted into the 30517th child. In this child tree, we split the bits again into 10010100 (148) and 00000000 (0). Zero is inserted into the 148th child, which happens again for two move levels (0000 and 00) before the base case of a one bit vEB, which just stores the 0. It breaks down as follows:
01110111001101011001010000000000
Summary: 30517 0111011100110101
Cluster[30517]:
Summary: 148 10010100
Cluster[148]:
Summary: 0 0000
Cluster[0]:
Summary: 0 00
Cluster[0]:
Summary: 0 0
Cluster[0]: 0 0
Each summary tree would similarly break down the number stored there. Conceptually, it's much like a trie over the bits of the number. Inserting 2,000,000,001 into this same tree would not require allocating any additional objects, as it would result in all the same summary entries, and would simply insert a 1 instead of a 0 in the final cluster. The Wikipedia entry points out that initially, the space usage is not very efficient (as each entry needs to create about log(w) new trees), but as the tree grows in size, more of these trees are reused.
I created an implementation in Python and shared on Github. Erik Demaine at MIT also covers van Emde Boas trees in 6.851 (Lecture 11). It is much of the same material, and Dr. Demaine is a great lecturer, so I find it valuable. I'd hoped he would cover y-fast trees, but alas he mostly focused on vEB trees.
x, y fast tries
Another data structure that solves the predecessor problem is the y-fast trie (which both Nelson and Demaine are quick to attribute to Willard). The y-fast trie builds upon the x-fast trie, which was introduced in the same paper and really just serves as a component in the y-fast trie.
Conceptually, think of this data structure as a bit vector v of size U. If x is in the set, then v[x] = 1, and all other values are zero. To facilitate predecessor and successor, we put all the ones in a doubly linked list.
We want better than O(U) time, so we construct a complete binary tree over our bit vector, with values being the OR of their child nodes. Each node also has a pointer to the min and max value in its subtree. We now have a tree of depth lg U (i.e. w), but this still isn't good enough. Rather than traverse up and down each level of the tree, we do a binary search on the levels of the tree, looking for the first one. We can do this because the values on the path from any given value to the root is monotonic; once a value is 1, all its parents will be one. Having found the first one, we can follow the pointer to the min or max (and maybe one more hop to get to the pred or succ, depending on what we needed and what was available).
Nelson describes how this could be done with a binary heap (only as a lead up to the better bounds described below), whereas the Wikipedia page describes a bitwise trie arrangement (which is also the way Demaine describes it).
While this gives us our desired query bound, updates are slow, and we are still taking up O(U) space. We can reduce the space complexity by keeping only the linked list of ones (no bit vector), and using hash tables to store the ones on each level of the tree. This reduces space to O(nw). But updates are still O(w) (not lg w). This is where the y-fast trie comes into play.
Using a technique called indirection, we reduce space and time complexity by combining the x-fast trie with balanced bsts. Rather than store all n items in the x-fast trie, we have n/w "representative items". Dangling off these representative items are bst's containing O(w) items each. Inserting into a leaf tree only takes O(lg w) time. Updates to the x-fast trie still takes O(w) time, but we can amortize these operations to the O(w) insertions that took place in the bst that made it necessary to resize (so we basically get them for free).
For space, each bst takes Θ(w) space, and there are n/w of them, giving us O(n/w * w) or O(n) space for the trees. The math for the x-fast space is similar. Structureally the x-fast trie requires O(nw) space, but "n" in this context is the "representative items", of which there are n/w, so we again get O(n/w * w) or O(n) space.
Fusion Trees
The last data structure discussed for the predecessor problem (and also covered in 6.851) is the fusion tree. The fusion tree is built around several ideas:
- k-ary tree structure
- word level parallelism
- sketch compression
- most significant set bit (MSB) in O(1)
The fusion tree is a k-ary tree (i.e. a b-tree) where k is equal to w raised to some fractional power (both Nelson and Demaine use w ^ 1/5). Concretely, this means that if w is 1024, when k would be 4. It took me several iterations through the lectures to wrap my head around why they chose such a small power (even the original paper was little help). However, these two slide decks from Stanford (Fusion Trees: part 1, part 2) do a good job of working through the concepts step by step. The worked examples really helped me understand what was happening.
The height of the tree is log base w of n (I'm going to abbreviate this as log_w n from here on out), which means that in order to achieve log_w n query, we can only afford to do O(1) work in each node. We can do any operation on a single word in constant time, but our O(k) keys do not fit in a single word (4 * 1024 > 1024... duh). So we have to compress these keys. The intuition that Demaine notes here is that since we only have O(k) keys, we only need k - 1 bits to differentiate them. The visualization both lecturers use is to represent the keys as a path in a binary tree:
The Stanford slides describe the sketch as a Patricia Trie, but it works out to the same thing. The sketches presented above are perfect sketches, meaning they contain exactly the r important bits for each entry. The problem with perfect sketches is that they cannot be computed in constant time, so an approximate sketch is needed that can still compress the keys enough to fit them all into a single word. This is a byproduct of using multiplication bit tricks, as it is required to avoid collisions when shifting bits around. It turns out that you can prove that r^4 works (which is w^4/5, or on our 1024 bit machine, 256 bits). So our w^1/5 sketches of size w^4/5 bits will just fit into a w size word. Tada!
Now, when we have a query q come into our tree, we have to "desketch" in order to make the right decision about where it ranks. This is because the bits in q were not used to build our decision tree, and at some point q "falls off" the tree. Imagine the number 1010 coming into the tree above. It's sketch contains b1 and b3 (zero indexed from the right), so it would be 11, placing it between 1100 and 1111, which obviously isn't right. The solution is to determine where q fell off, and construct an alternate representation, e, that replaces the bits after the falling off point with either ones or zeros (depending on which direction q fell off).
To compute e, we first compute y, which is the longest common prefix between q and the key sketch(q) led us to. Nelson offers one way to compute where q falls off, which is to take the MSB of q with xi and xi+1, and take the most significant of the two (y is the bit before this bit). I liked the way Demaine explained this, basically saying we want a representative value to substitute for q that is either the max of the left subtree or the min of the right subtree, depending on which way we fell off. If we fell off to the left, we want e to be y followed by 1 (we want our representative in the right subtree) followed by 0s (we want the min element). Had we fallen off to the right, the logic is reversed.
The bit fiddly tricks necessary to get all this to work were quite interesting, and I think arguably one of the more useful takeaways. "Fusing" multiple small numbers into a single word so we can do parallel addition, comparison, and ranking is quite nifty (I think the Stanford slides have the best illustrations of this, as part of explaining the "sardine tree" haha).
Willard notes in his original paper that the fusion tree is of theoretical interest only and is not practical. Thinking about the numbers a bit, it's not hard to agree with this assessment. In our 1024 bit w machine, we still only put 4 keys in a node. While it is a constant number of operations to perform the parallel rank, that constant number is still larger than lg 4. If we wanted to have k = 8, our word size w would need to be 32,768!
Hashing (CS224, Lectures 3 - 5)
The next few lectures deal with hashing, which is a technique for mapping a universe U to a (generally) smaller set m. Nelson runs through the material pretty quickly, so I found it helpful to lean on additional sources of information to fully appreciate. I tried to find original papers where I could, and generally the wiki pages were a good resouce as well. Both sets of 6.854 lectures had at least one very relevant session on hashing (Karger lecture 7, Moitra lecture 3, part 2)
CLRS Chapter 11: Hash Tables is a good refresher. It describes the dictionary problem, i.e. we have a keys and their associated items, and we need a way to store these key-value pairs efficiently while also providing fast INSERT, DELETE and FIND operations. Assuming keys are integers, one solution is to use an array, with the key being the index of the item. While operations are fast, O(1), the storage requirement is absurd, requiring an array of size O(U). A better option would be to use an array of size m, which is some constant factor larger than n, the number of items. Instead of indexing directly into the array, we use a hash function h() to transform our key into a index.
In order to ensure good average behavior of our hash function based datastructures, we can't rely on a single hash. Instead, we need to develop a family of hash functions H. Because we are mapping from a large universe into a smaller array, it is inevitable that there will be collisions, values for which h(x) = h(y). This means that for any given single hash function h(), there is a pathological set of inputs that all map to the same value, which leads to catastrophic failure of our assumptions (kiss your O(1) lookup goodbye). By choosing our hash function uniformly at random from H, we get good expected behavior across any given set (i.e. it's impossible for an adversary to pick a pathological set, though such sets do still exist). This idea is called universal hashing [paper].
Resolving collisions can be done different ways, the two high level schemes being chaining and open addressing. In chaining, when two values map to the same index, they are placed in a "bin". This may be a linked list, but other strategies are possible (the OpenJDK HashMap implementation starts with linked lists and switches to trees when bins get large enough to justify the overhead).
Open addressing schemes use only one item per slot, but are more flexible with how they decide which items go where. Probing schemes (such as linear probing [paper]) will start looking for a slot at h(k), and if that place is already occupied will search through the array for the next available slot. Linear probing does this one index at a time, which makes it a cache friendly scheme (and thus fast in practice), but it also makes it vulnerable to clustering. I found an implementation by Sedgewick etal from Princeton that uses linear probing as a contrast to the Java HashMap.
Another scheme for open addressing is cuckoo hashing [paper]. With cuckoo hashing, two hash functions are used instead of one. When inserting a new item, the locations produced by each of these two hash functions are checked first. If both are full, the item "kicks out" one of the existing items. That item then falls back to the location given by its other hash function, which may also result in a value being kicked out. The number of evictions is capped (it's possible to end up in an infinite cycle), and when the cap is reached, two new hash functions are chosen and the hash table is rebuilt.
(good candidate for implementation)...
One of the questions that the advanced algorithms classes tackle that is glossed over in lower level algo classes is "what is the expected load in the biggest bucket". All three sets of lectures make at least passing reference to a concept called "balls in bins", which is a probability problem that imagines we have n balls that are randomly dropped into n bins. I found a short lecture from NPTEL that explains the problem specifically, using the birthday problem (with which we get a bound of √n, this SO question was helpful). With full independence, we can get a tighter bound: with high probability, the bin with the largest load (the longest linked list in a hash table with chaining, for example) will have O( log n / log log n) items. This log over log log factor pops up in several other analysis.
One way to improve upon this maximum load is using a technique called "the power of two choices" [wiki][paper] (Nelson covers this midway through lecture 5). In this scheme, instead of a single hash function, two functions are used. Items are mapped to the "least loaded" of the two bins. This reduces the max load to just O( ln ln n / ln 2). While schemes using >2 choices are possible, they only change the base of the log, for a constant factor improvement, so they aren't really all that interesting.
A technique used by just about all the lecturers to analyze hashing is the Chernoff bound. Just as you need to know what a crumpet is to understand cricket, you need to understand the Markov Inequality to understand Chernoff bounds. Tom Leighton does a great job explaining both (along with Chebyshev's inequality) in lecture 24 of 6.042. Now, in order to use the Chernoff bound, we must be able to represent the problem being bound as a series of mutually independent random variables.
In Karger's lecture, he makes the observation that having mutual independence between the items is actually quite a lot of randomness. In order for a hash function to behave as if it is fully random, it is sufficient that to have a pairwise independent family of hash functions.
The concrete example used, well basically everywhere, is a polynomial in the for ax + b. "a" and "b" define the hash function and are chosen at random. Taking the result mod p, where p is some prime larger than u, we get a distribution uniform in p. Taking this mod m, we then get a distribution approximately uniform in the size of our hash table array (both Karger and Nelson explain why we get a distribution slightly skewed to the beginning of our range m). Basically, because p is prime, it is not a multiple of m, so there is some "slop" or "slush" after all but the last size m factor is divided out of p.
Karger notes that while a 2-wise (pairwise) family is sufficient to get constant time operations in expectation when using chaining, we do worse on our expected largest bucket, which can be as large as √n, rather than the log over loglog bound that we achieved with mutual independence. Nelson covers the more general idea of k-wise independent hash functions, a discussion that segues into linear probing, which actually requires at least 5-wise independence to guarantee constant time per operation (some 4-wise independent hash functions can end up taking O(log n) apparently).
The intuition that I found helpful for understanding this is polynomial interpolation (i.e. curve fitting). Given k + 1 points (evaluations of h(x), say), there is exactly one degree k polynomial that fits that curve. So if we are using a degree 2 polynomials as our hash family, and h_1(x1, x2, x3) = h_2(x1, x2, x3), then we know the functions are equivalent and will collide on every value of x, whereas if these functions were truly random, these three collisions would tell us nothing about the value of h(x4).
The dictionary problem is not the only one that can be solved with hashing. Membership, or at least approximate membership, can be solved using a technique called Bloom filters [paper]. Where a typical dictionary (HashMap in Java, dict in Python, etc.) uses at O(n * lg U) bits (since we are storing n keys of lg U bits each), a Bloom filter aims to reduce this storage requirement, with the trade off being that there might be false positives when querying for membership.
The bloom filter starts off life as a bit array. For each element in our set, we use a hash function to determine the index for that element in the bit array and set the value to one. If our bit array is size at least 2n, then our expected false positive rate is about 50%, which isn't great. However, we can use multiple bit arrays to make this probability arbitrarily small. For instance, if we want 25% false positive rate, we would use 2 bit arrays, each with their own hash function. Setting a value in the set is done by setting the bit for h_i(x) in each of the tables, and querying membership means checking each table.
Since each table gives us ~50% false positive rate, we would need both tables to trick us, which is 50% x 50%. Generally, we need log_2 ( 1 / e ), where e is our error rate. So if we want no worse than a 1% expected false positive rate, we need log_2( 1 / .01 ) = log_2( 100 ) ≈ 7. Another way to think of this is "how many times to I have to divide the rate in half to get my desired rate?". 7 arrays gives us 1 / (2^7) or 1/128, less than our target rate of 1%.
Nelson briefly touches on a data structure called a "Bloomier filter", although what he describes doesn't seem to align with what was described in the original paper. It seems more like the "cuckoo filter" Micheal Mitzenmacher describes in this talk. Michael's blog My Biased Coin and the Cuckoo Filter paper are additional resources on the topic. I particularly liked Michael's practical data comparing the performance of bloom filters with some of the more sophisticated variants.
At around minute 54 of the Karger lecture he discusses perfect hashing [paper]. A perfect hash function is one in which each item hashes to exactly one slot, i.e. there are no collisions. The birthday paradox tells us that if we map n items randomly into n^2 space, the probability of a collision is 50%. This means our hash function, naively, would need quadratic space. The solution is to use a multi level approach. On the top level, we have n items and n buckets, and use a standard pairwise independent hash function.
In each bucket, we use b^2 space to store the keys using a second hash function. In order to get O(n) overall space, none of the buckets can be too big; the solution is to try different hash functions until one is found that works well. The expected space for the second level is O(n^2 / s ), where s is the set and n is the size of the top level hash function. Given this expectation, we see that setting n = s gives us O(n) space for the second level (though the constants are pretty brutal if you aren't really clever, apparently).
CLRS Chapter 11: Hash Tables is a good refresher. It describes the dictionary problem, i.e. we have a keys and their associated items, and we need a way to store these key-value pairs efficiently while also providing fast INSERT, DELETE and FIND operations. Assuming keys are integers, one solution is to use an array, with the key being the index of the item. While operations are fast, O(1), the storage requirement is absurd, requiring an array of size O(U). A better option would be to use an array of size m, which is some constant factor larger than n, the number of items. Instead of indexing directly into the array, we use a hash function h() to transform our key into a index.
In order to ensure good average behavior of our hash function based datastructures, we can't rely on a single hash. Instead, we need to develop a family of hash functions H. Because we are mapping from a large universe into a smaller array, it is inevitable that there will be collisions, values for which h(x) = h(y). This means that for any given single hash function h(), there is a pathological set of inputs that all map to the same value, which leads to catastrophic failure of our assumptions (kiss your O(1) lookup goodbye). By choosing our hash function uniformly at random from H, we get good expected behavior across any given set (i.e. it's impossible for an adversary to pick a pathological set, though such sets do still exist). This idea is called universal hashing [paper].
Resolving collisions can be done different ways, the two high level schemes being chaining and open addressing. In chaining, when two values map to the same index, they are placed in a "bin". This may be a linked list, but other strategies are possible (the OpenJDK HashMap implementation starts with linked lists and switches to trees when bins get large enough to justify the overhead).
Open addressing schemes use only one item per slot, but are more flexible with how they decide which items go where. Probing schemes (such as linear probing [paper]) will start looking for a slot at h(k), and if that place is already occupied will search through the array for the next available slot. Linear probing does this one index at a time, which makes it a cache friendly scheme (and thus fast in practice), but it also makes it vulnerable to clustering. I found an implementation by Sedgewick etal from Princeton that uses linear probing as a contrast to the Java HashMap.
Another scheme for open addressing is cuckoo hashing [paper]. With cuckoo hashing, two hash functions are used instead of one. When inserting a new item, the locations produced by each of these two hash functions are checked first. If both are full, the item "kicks out" one of the existing items. That item then falls back to the location given by its other hash function, which may also result in a value being kicked out. The number of evictions is capped (it's possible to end up in an infinite cycle), and when the cap is reached, two new hash functions are chosen and the hash table is rebuilt.
(good candidate for implementation)...
One of the questions that the advanced algorithms classes tackle that is glossed over in lower level algo classes is "what is the expected load in the biggest bucket". All three sets of lectures make at least passing reference to a concept called "balls in bins", which is a probability problem that imagines we have n balls that are randomly dropped into n bins. I found a short lecture from NPTEL that explains the problem specifically, using the birthday problem (with which we get a bound of √n, this SO question was helpful). With full independence, we can get a tighter bound: with high probability, the bin with the largest load (the longest linked list in a hash table with chaining, for example) will have O( log n / log log n) items. This log over log log factor pops up in several other analysis.
One way to improve upon this maximum load is using a technique called "the power of two choices" [wiki][paper] (Nelson covers this midway through lecture 5). In this scheme, instead of a single hash function, two functions are used. Items are mapped to the "least loaded" of the two bins. This reduces the max load to just O( ln ln n / ln 2). While schemes using >2 choices are possible, they only change the base of the log, for a constant factor improvement, so they aren't really all that interesting.
A technique used by just about all the lecturers to analyze hashing is the Chernoff bound. Just as you need to know what a crumpet is to understand cricket, you need to understand the Markov Inequality to understand Chernoff bounds. Tom Leighton does a great job explaining both (along with Chebyshev's inequality) in lecture 24 of 6.042. Now, in order to use the Chernoff bound, we must be able to represent the problem being bound as a series of mutually independent random variables.
In Karger's lecture, he makes the observation that having mutual independence between the items is actually quite a lot of randomness. In order for a hash function to behave as if it is fully random, it is sufficient that to have a pairwise independent family of hash functions.
The concrete example used, well basically everywhere, is a polynomial in the for ax + b. "a" and "b" define the hash function and are chosen at random. Taking the result mod p, where p is some prime larger than u, we get a distribution uniform in p. Taking this mod m, we then get a distribution approximately uniform in the size of our hash table array (both Karger and Nelson explain why we get a distribution slightly skewed to the beginning of our range m). Basically, because p is prime, it is not a multiple of m, so there is some "slop" or "slush" after all but the last size m factor is divided out of p.
Karger notes that while a 2-wise (pairwise) family is sufficient to get constant time operations in expectation when using chaining, we do worse on our expected largest bucket, which can be as large as √n, rather than the log over loglog bound that we achieved with mutual independence. Nelson covers the more general idea of k-wise independent hash functions, a discussion that segues into linear probing, which actually requires at least 5-wise independence to guarantee constant time per operation (some 4-wise independent hash functions can end up taking O(log n) apparently).
The intuition that I found helpful for understanding this is polynomial interpolation (i.e. curve fitting). Given k + 1 points (evaluations of h(x), say), there is exactly one degree k polynomial that fits that curve. So if we are using a degree 2 polynomials as our hash family, and h_1(x1, x2, x3) = h_2(x1, x2, x3), then we know the functions are equivalent and will collide on every value of x, whereas if these functions were truly random, these three collisions would tell us nothing about the value of h(x4).
The dictionary problem is not the only one that can be solved with hashing. Membership, or at least approximate membership, can be solved using a technique called Bloom filters [paper]. Where a typical dictionary (HashMap in Java, dict in Python, etc.) uses at O(n * lg U) bits (since we are storing n keys of lg U bits each), a Bloom filter aims to reduce this storage requirement, with the trade off being that there might be false positives when querying for membership.
The bloom filter starts off life as a bit array. For each element in our set, we use a hash function to determine the index for that element in the bit array and set the value to one. If our bit array is size at least 2n, then our expected false positive rate is about 50%, which isn't great. However, we can use multiple bit arrays to make this probability arbitrarily small. For instance, if we want 25% false positive rate, we would use 2 bit arrays, each with their own hash function. Setting a value in the set is done by setting the bit for h_i(x) in each of the tables, and querying membership means checking each table.
Since each table gives us ~50% false positive rate, we would need both tables to trick us, which is 50% x 50%. Generally, we need log_2 ( 1 / e ), where e is our error rate. So if we want no worse than a 1% expected false positive rate, we need log_2( 1 / .01 ) = log_2( 100 ) ≈ 7. Another way to think of this is "how many times to I have to divide the rate in half to get my desired rate?". 7 arrays gives us 1 / (2^7) or 1/128, less than our target rate of 1%.
Nelson briefly touches on a data structure called a "Bloomier filter", although what he describes doesn't seem to align with what was described in the original paper. It seems more like the "cuckoo filter" Micheal Mitzenmacher describes in this talk. Michael's blog My Biased Coin and the Cuckoo Filter paper are additional resources on the topic. I particularly liked Michael's practical data comparing the performance of bloom filters with some of the more sophisticated variants.
At around minute 54 of the Karger lecture he discusses perfect hashing [paper]. A perfect hash function is one in which each item hashes to exactly one slot, i.e. there are no collisions. The birthday paradox tells us that if we map n items randomly into n^2 space, the probability of a collision is 50%. This means our hash function, naively, would need quadratic space. The solution is to use a multi level approach. On the top level, we have n items and n buckets, and use a standard pairwise independent hash function.
In each bucket, we use b^2 space to store the keys using a second hash function. In order to get O(n) overall space, none of the buckets can be too big; the solution is to try different hash functions until one is found that works well. The expected space for the second level is O(n^2 / s ), where s is the set and n is the size of the top level hash function. Given this expectation, we see that setting n = s gives us O(n) space for the second level (though the constants are pretty brutal if you aren't really clever, apparently).
The last concept covered by the hashing lectures is consistent hashing [paper]. Developed by Tom Leighton et. al. at MIT, it became the basis of Akamai's competitive advantage. The first lecture by Moitra (part 1, part 2) covers this in depth. The basic intuition is that the hash function maps items and machines into the range of real numbers in [0,1]. Items are then assigned to machines based on the proximity of the hash value (either closest, or all to right, it amounts to the same analysis). What this means is that when we need to resize the hash table (that is, add a new machine), we only need to rehash a small portion of the table instead of the entire thing.
Compare this to a hash table using a modular arithmetic based hash function. When we need to resize the backing array to accommodate more items, we basically need to create a whole new array and rehash all the existing items back into it. With consistent hashing, when a node is added, only K/n items need rehashing (where K is the number of keys and n the number of nodes). Well I think I'm about funned out on hashing...
Amortized analysis came up while I was working on 6.046. It's covered in chapter 17 of CLRS, and my post on 6.046 gives a brief synopsis of the various methods. For this class, both Nelson and Karger analyze data structures with interesting amortized behavior. Nelson covers Fibonacci heaps (Karger probably does too in one of the missing lectures), and both cover Splay Trees. Both use the
potential function method extensively for analyzing both data structures.
The potential function method works by defining a potential function, typically signified by φ (phi), to map the state of the data (S) to a positive real number. This function should be zero for a newly initialized state S_0. The amortized time for a single operation is defined as T_amort(o) = T_actual(o) + φ(S_after) - φ(S_before). For a series of operations O, the potential function values telescope, so the result is that the amortized sum for a series of operations only requires the first and last potential function values: T_amort(O) = T_actual(O) + φ(S_n) - φ(S_0). Because φ(S_0) = 0 and φ(S_n) ≥ 0, the amortized cost can give us a valid upper bound on the actual cost.
Fibonacci Heap visualization from University of San Francisco.
Fibonacci Heaps are a priority queue data structure developed by Fredman and Tarjan in 1984 and published in 1987, and conveniently covered by chapter 19 in CLRS. Nelson explains F-heaps by first covering binomial heaps [Brilliant][wiki][visualization]. A binomial heap supports the standard Heap AST operations: insert, decrease-key, delete-min, etc. Unlike a binary heap, which is a single (mostly) complete binary tree, a binomial tree is actually a forest with the following properties:
In analyzing the amortized cost of the F heap, we define the potential function φ = T(H) + 2M(H), where T(H) is the number of trees in the root, and M(H) is the number of "marked" nodes.
Fibonacci heaps have a reputation for being slow in practice. I found several papers that seem to support this conventional wisdom:
Splay Tree visualization from University of San Francisco.
The splay tree is a binary search tree created by Tarjan and Sleator in 1985, described in their paper "Self Adjusting Binary Search Trees". What is remarkable about the splay tree is that it achieves the same bounds for BST operations as other balanced trees such as AVL and red-black trees, and does so with no auxiliary information whatsoever. Not only that, but it also achieves several other interesting properties.
Splay trees have a very fluid internal structure. The key to this fluidity, and the foundation of its self adjusting nature, is the "splay" operation. Whenever a value is inserted, deleted, or searched for in the splay tree, a series of double rotations is performed to bring that node to the root. The structure of the tree determines exactly which type of double rotation is performed.
When the parent and grandparent of the node being splayed are on the same side, the double rotation (called a "zigzig") essentially "flips" the nodes:
When the parent and grandparent alternate sides, a "zigzag" operation puts the ancestors on either side of the splayed node:
In the case where the number of nodes on the path from the target node to the root is odd, a final single rotation follows these double rotations.
Nelson and Karger both use amortized analysis to describe the run time. Karger explains the "access lemma" pretty much the same way it was explained in the original paper, which Nelson offers an alternate proof based on AMGM. The potential function used in the analysis centers on the function r(x), which is defined as lg(size of the tree at node x). The potential function for splay trees is shown to be bounded by 3(r(t) - r(x)) + 1, where t is the tree and x is some node in t being splayed to the root. This results in an amortized time of O(log(s(t)/s(x)).
In lecture 5, Karger explains how a splay tree does insertions and deletions. Insertion involves first descending the tree to play the item in the correct position, followed by splaying the item back up to the root. In order to support deletion, the splay tree also supports the split and merge operations. The split operations breaks a splay tree into two trees (at the root), while a merge joins two splay trees. With these two operations, deletions are accomplished by splaying the node to be deleted down to the root, splitting it from both sub trees, then merging the child trees to each other (making the maximum item in the smaller tree the new root).
Online Algorithms (CS224, Lectures 8 - 10)
Compare this to a hash table using a modular arithmetic based hash function. When we need to resize the backing array to accommodate more items, we basically need to create a whole new array and rehash all the existing items back into it. With consistent hashing, when a node is added, only K/n items need rehashing (where K is the number of keys and n the number of nodes). Well I think I'm about funned out on hashing...
Amortized Analysis (CS224, Lectures 6 - 7)
Amortized analysis came up while I was working on 6.046. It's covered in chapter 17 of CLRS, and my post on 6.046 gives a brief synopsis of the various methods. For this class, both Nelson and Karger analyze data structures with interesting amortized behavior. Nelson covers Fibonacci heaps (Karger probably does too in one of the missing lectures), and both cover Splay Trees. Both use the
potential function method extensively for analyzing both data structures.
The potential function method works by defining a potential function, typically signified by φ (phi), to map the state of the data (S) to a positive real number. This function should be zero for a newly initialized state S_0. The amortized time for a single operation is defined as T_amort(o) = T_actual(o) + φ(S_after) - φ(S_before). For a series of operations O, the potential function values telescope, so the result is that the amortized sum for a series of operations only requires the first and last potential function values: T_amort(O) = T_actual(O) + φ(S_n) - φ(S_0). Because φ(S_0) = 0 and φ(S_n) ≥ 0, the amortized cost can give us a valid upper bound on the actual cost.
Fibonacci Heaps
Fibonacci Heap visualization from University of San Francisco.
Fibonacci Heaps are a priority queue data structure developed by Fredman and Tarjan in 1984 and published in 1987, and conveniently covered by chapter 19 in CLRS. Nelson explains F-heaps by first covering binomial heaps [Brilliant][wiki][visualization]. A binomial heap supports the standard Heap AST operations: insert, decrease-key, delete-min, etc. Unlike a binary heap, which is a single (mostly) complete binary tree, a binomial tree is actually a forest with the following properties:
- each tree has a "rank", which is equal to the degree of the tree's root.
- the number of nodes in a tree is 2^k (k = rank)
- each tree has a unique rank.
- each child of the root of a tree has ranks from 0 to k-1.
Each tree in the forest can be thought of as a bit in a bit vector of length lg(n). The first step in insert(x) is to create a singleton tree containing x. If a tree of rank 0 is already in the tree, the two are merged (maintaining the heap property). If a tree of rank 1 already exists as well, then the merge "carries" much like in binary addition. This continues until no tree of rank k is already present. In the worst case, insert can take O(lg n) if the forest is "full", i.e. trees of rank 0 - lg(n) already exist.
For Fibonacci heaps, we take the binomial heap concepts and make them "lazy":
- When inserting, do not merge trees
- When decreasing key, one of two cases:
- New value does not violate heap property, i.e. still greater than parent.
- New value is less than parent. In this case, cut it out and make a top level tree.
While F heaps loosen the requirement around how many nodes are in each tree, they don't eliminate them entirely. Whenever a node loses a child, it gets a "mark". When a second child is removed, we remove the marked parent as well and make it a root node. This can create a series of "cascading cuts" when we have a series of marked ancestors. This has the effect of creating trees that contain at least the d+2 Fibonacci number.
In the below figure, the red outlined nodes can be cut without triggering a cascading delete or changing the degree of the root. After the outlined nodes are cut the blue nodes are all "marked":
In analyzing the amortized cost of the F heap, we define the potential function φ = T(H) + 2M(H), where T(H) is the number of trees in the root, and M(H) is the number of "marked" nodes.
Fibonacci heaps have a reputation for being slow in practice. I found several papers that seem to support this conventional wisdom:
- Comparison of Fibonacci Heaps and 2-3 heaps for Dijkstra: 1999 paper.
- Empirical study of several heap implementations: 2014 paper.
- Optimizing Dijkstra for real-world performance: 2015 paper.
Splay Trees
Splay Tree visualization from University of San Francisco.
The splay tree is a binary search tree created by Tarjan and Sleator in 1985, described in their paper "Self Adjusting Binary Search Trees". What is remarkable about the splay tree is that it achieves the same bounds for BST operations as other balanced trees such as AVL and red-black trees, and does so with no auxiliary information whatsoever. Not only that, but it also achieves several other interesting properties.
Splay trees have a very fluid internal structure. The key to this fluidity, and the foundation of its self adjusting nature, is the "splay" operation. Whenever a value is inserted, deleted, or searched for in the splay tree, a series of double rotations is performed to bring that node to the root. The structure of the tree determines exactly which type of double rotation is performed.
When the parent and grandparent of the node being splayed are on the same side, the double rotation (called a "zigzig") essentially "flips" the nodes:
When the parent and grandparent alternate sides, a "zigzag" operation puts the ancestors on either side of the splayed node:
In the case where the number of nodes on the path from the target node to the root is odd, a final single rotation follows these double rotations.
Nelson and Karger both use amortized analysis to describe the run time. Karger explains the "access lemma" pretty much the same way it was explained in the original paper, which Nelson offers an alternate proof based on AMGM. The potential function used in the analysis centers on the function r(x), which is defined as lg(size of the tree at node x). The potential function for splay trees is shown to be bounded by 3(r(t) - r(x)) + 1, where t is the tree and x is some node in t being splayed to the root. This results in an amortized time of O(log(s(t)/s(x)).
In lecture 5, Karger explains how a splay tree does insertions and deletions. Insertion involves first descending the tree to play the item in the correct position, followed by splaying the item back up to the root. In order to support deletion, the splay tree also supports the split and merge operations. The split operations breaks a splay tree into two trees (at the root), while a merge joins two splay trees. With these two operations, deletions are accomplished by splaying the node to be deleted down to the root, splitting it from both sub trees, then merging the child trees to each other (making the maximum item in the smaller tree the new root).
Online Algorithms (CS224, Lectures 8 - 10)
Online algorithms deal with making decisions in the face of uncertainty (almost directly quoting Nelson here). They deal with problems where not all the data is known ahead of time. A real world example is cache invalidation (one of the two hardest problems in computer science). In addition to Nelson's lectures, Erik Demaine subs for Karger in lecture 24 of the MIT version of the class and discusses many of the same concepts.
The measure of how good a given online algorithm performs is often expressed as a "competitive ratio". The numerator in this ratio is the online algorithm, while the denominator is the performance of the optimum algorithm (OPT), which is often assumed to have full knowledge of the future. The concept is credited to Sleator & Tarjan, who described it in a paper in 1985.
Both profs make a point of describing the different types of adversaries used to model our worst case performance (around 1:12:00 mark in lecture 8 for Nelson, 32:00 mark for Demaine):
- Oblivious: (weak adversary) knows what algorithm you are using, but knows nothing about the past or future coin flips. Primary model used for analysis.
- Adaptive: (online) sees the past but does not know the future.
- Omniscient: (fully adaptive) sees all the coin flips, past and future, so your randomized algorithm is basically deterministic.
The "Ski Rental Problem" is used by both Nelson and Demaine to explain competitive analysis. The problem sets up like this: you are going skiing with a group of friends for an indefinite duration. Renting skis for a day costs $1, and buying a set of skis costs $b. You wake up each morning and find out if you will be skiing or going home. The question is, when do you buy skis?
OPT knows how many days you will be skiing: if it's more than b days, you buy skis, otherwise you rent every day, so you never pay more than b. We don't have this luxury of perfect foresight, and we want to minimize regret. That is, the difference between our decisions, and the decisions we'd have made in hindsight. The best deterministic strategy will rent skis for b days, then buy. With this strategy, we never pay more than 2b, so the algorithm is said to be 2 competitive.
A more real-worldy application of this kind of analysis is cache paging [paper]. The idea is we have a two tiered memory system (L1 cache and main memory, or main memory and disk, etc), where one tier is orders of magnitude slower than the other. To maximize performance, we want to serve requests from the faster cache as much as possible, but since this cache is relatively small, we sometimes have to bring items in from slow memory. If the cache is full, we need to evict something already in the cache. One well known eviction strategy is Least Recently Used (LRU), another is First In First Out (FIFO). Wikipedia has a list of other cache replacement policies, but it is enough to know these for now.
The optimal theoretical algorithm is furthest in the future (Belady's algorithm, clairvoyant algorithm), which evicts the item from the cache that goes the longest time until it needs to be brought back into the cache. This means that for a cache size k, if there are k + 1 items (only one item is not in the cache at a time), you only have a cache miss every 1/k requests.
In this model, It turns out that the best competitive ratio any deterministic algorithm can achieve is k. If you have a 8gb cache, this is a pretty terrible ratio (I chuckle every time I hear Nelson say "8 billion competitive"). This is because for any deterministic algorithm an adversary can always request the cache item that was just evicted and you get a cache miss for every request. Randomized algorithms do much better (for non-omniscient adversaries anyway), achieving a log(k) competitive ratio.
Resource Augmentation [download original paper][related paper] is an alternative way of analyzing online algorithms that relaxes the constraints. Basically, we give our online algorithms more resources: more machines, more time, whatever. In the cache paging problem, if we make the cache twice as large as the offline optimal algorithm, we get a 2 competitive algorithm instead of a k competitive algorithm (at least for FIFO and LRU), which is much better if your cache is O(millions) of cache lines.
Tim Roughgarden goes deeper on the subject in Stanford CS354 (notes)
[Side Note]
The wikipedia page for the ski rental problem describes a randomized algorithm that does better in expectation than 2, achieving an e/e-1 ratio (roughly 1.58). Basically how the algorithm works is that every day up to b you flip a coin using a certain distribution (it would not be pretty here, look it up on the wiki page). I was curious what this distribution actually looked like so I plugged it into a Google Sheet and charted it:
Nelson mentions it in while describing the primal/duel framework.
Primal/Duel LP
Some references:
LP Primal Duel Framework (Ad Auctions and TCP Acks): Buchbinder, Jain, Naor, [paper]
Online Primal-Dual Algorithms for Covering and Packing [paper]
Strongly Competitive Randomized Paging [paper]
Competitive Paging Algorithms (Mark) [paper]
Online set cover: [paper]
In lecture 9, Nelson describes a paging algorithm called "Mark". The algorithm is pretty straightforward:
Think of the algorithm as working over a series of "phases". At the beginning of a phase, all the items in the cache are unmarked. When items are put in the cache (or items still in the cache are accessed), they are "marked". When items are brought into the cache, they evict an unmarked item uniformly at random. This algorithm is 2H(k) competitive, that is 2 x (kth harmonic number). Harmonic numbers are approximated by the natural log, so if k = 8 billion (main memory vs disk example), then our algorithm is about 2 * 22.8 ≈ 46 competitive.
Jelani introduces the "Primal/Duel framework" for analyzing online algorithms. The way this works is that we define a linear program for the thing we want to minimize (money spent on ski's perhaps), and then use the property of weak duality to define upper and lower bounds on the competitive ratio based on the primal and duel solutions. Karger covers duality in lecture 15 of the MIT series, providing an interesting analogy to physics to color our intuition. He also shows how to get the duel for an arbitrary LP (vs a Standard Form LP). Karger works some examples in lecture 16.
[At this point I'm fully out of gas for taking notes, so don't expect in-depth analysis from here, rather mostly links to references and quick summaries. It doesn't help that much of the remainder of the class leans so heavily on LP which, sorry, I don't find terribly interesting...]
Some of the basic vocabulary for approximation algorithms was introduced in 6.046, so I'll keep it pretty brief here:
Knapsack has straightforward DP solutions that run in pseudo polynomial time. They aren't true poly solutions because they rely on the size of the input W, which is represented by lg(W) bits. Fortunately it does admit a FPTAS. First we look at some greedy algorithms.
The first approximation algorithm Jelani suggests is a greedy algorithm that sorts the items by value ratio and takes items till no more will fit. However, this naive algorithm can do quite terrible. Imagine we have two items with the following weights and values:
Item 1 has a slightly better value ratio and gets picked first, but then item 2 won't fit, so we get a W competitive algorithm, blech! We can improve this by taking modifying our algorithm so that we take either the output of greedy, OR the most valuable item, at every step. This gives us a 2 approximation.
A PTAS for Knapsack goes like this: First, consider two observations -
So we select subset S, containing at most 1/ε items. These are the "big items". Remove any remaining items with value > anyone in S. Now run greedy on what is left over. We get an optimal approximation when we "guess" S correctly, so we just run this subroutine on all n^(1/ε) different subsets. Because epsilon is in the exponent of n, this is not an FPTAS. (the scribe notes were key to helping me understand what this algorithm was actually doing... "guess S, what??" lol).
Some problems don't admit an FPTAS, such as bin packing. For bin packing, this is due to the fact that even the decision problem formulation (i.e. "can these items fit in x bins") is NP-Hard. So if we have a 1 - ε approximation (say, "this bin packing uses 2.2 bins") then we can round this to the integral solution and then P == NP.
Next look at DNF Counting. DNF is similar to SAT (which is in CNF format). There is a polynomial time algorithm for finding DNF assignments, however the problem of counting all the possible satisfying assignments is NP-Hard (actually it is in a complexity class call #P, which is even harder).(FPRAS) due to KLM [paper]. The basic intuition of this algorithm is sampling: we make a random assignment to the items in the DNF and check if it is a satisfying assignment. The problem is that there may be an exponentially small number of satisfying assignments, which means we need to take exponential number of samples to get a good estimate. The workaround involves creating a surrogate set representing the original that is more amenable to sampling (I'm not even going to try to explain it, I don't really get it). The poly-n bounds are proved using Chernoff.
Semi-definite programming (Vandenberghe and Boyd [paper]) is touched on briefly. SDP is used by Goemans and Williamson [paper] to get a much better competitive ratio in Max Cut approximation (0.878 vs 0.5). The problem is formulated as a quadratic program, relaxed to vector dot products, solved yielding a bunch of unit vectors, which are then partitioned with a random hyperplane. Moitra spends all of lecture 19 [6.854 SP16] covering SDP and the Goemans-Williamson algorithm in much more depth.
## CS224 Lecture 13 is a guest lecture on unsupervised machine learning.
Karger covers approximation algorithms in lectures 19-22 of the MIT sequence. The remainder of this section are notes I took on the Karger lectures:
Absolute approximation are within some additive value of OPT. Planar graph coloring is an example. Any planar graph has a four coloring, so we need at most 4 colors, which would be at worst a 3 absolute approximation (we need at least one color). If the graph has an edge, we need at least two colors, making the 4 coloring a 2 approximation. However, if the graph has an odd cycle, then we need at least three colors, in which case the 4 coloring is a 1 approximation. In the case of a graph with no odd cycles, it it bipartite and can be colored with 2 colors.
Absolute approximations almost never exist. Karger explains this using a scaling argument: when we can scale the problem by the additive factor and solve, we end up within k/(k + 1), which basically gives us OPT (I'm probably butchering the explanation but that's the gist of it). Most approximations are described as being within a multiplicative factor α, called a relative approximation.
Greedy 2-approximate algorithm for Max-cut [wiki]: As you place a vertex, place it on the side of the cut with the minority of its placed neighbors. The best OPT can achieve is m, the number of edges in a graph (that is, a cut that goes through every edge), and because at every step we are creating at least as many cut edges as uncut edges, our approximation is at least 0.5 OPT (i.e. 1/α, α = 2, therefore "2 approximate").
Greedy Set Cover approximation achieves a O(ln n) ratio: At each step, we take the set that covers the most uncovered items. Suppose OPT = k (i.e. OPT uses k sets to cover all vertices), then there must be a set that covers n/k vertices in the first step. In each successive step at least a (1 - 1/k) portion of the remaining vertices are covered. When this portion is < 1, then the algorithm terminates. The wiki page includes an example where the approximation algorithm chooses three sets, where OPT would choose 2.
Greedy vertex cover achieves a 2 approximation: find an uncovered edge, and take both endpoints. Because OPT contains all edges, we know that at every step we are taking at least one vertex that is in OPT [wiki].
The scheduling problem involves putting j jobs on n machines for processing. Graham's algorithm (not called a "greedy algorithm" because apparently we didn't know about greedy algorithms yet) [1969 paper] acts in a greedy way by placing the jobs, in order, on the least loaded machine. This version of the algorithm achieves (2 - 1/m) OPT for the max load, and has the advantage of maintaining this ration even when jobs are coming online. The "Longest Processing Time" rule improves the ratio to 4/3, but this requires that we know all the jobs ahead of time. [slides I found useful]
Karger describes an algorithm for the P||C_max problem (scheduling j jobs on m machines that run in parallel, minimizing the max completion time). It is almost identical to the Knapsack approximation scheme.
Covers approximation of TSP. The naive MST approximation gets a 2 competitive ratio, but he also covers Christofides algorithm, which improves upon the MST based approximation by using a better rounding scheme. Instead of doubling up every edge (which yields the 2 approximation), it converts the MST into an Euler graph by matching up the odd degree vertices. This creates an Euler tour. Since we know that the MST is ≤ OPT, and a min-cost perfect bipartite matching of the odd vertices is ≤ OPT / 2, we get a 3/2 OPT approximation. Also mentions the Held-Karp bound [paper], but doesn't go into it.
Karger covers the LP relaxation of Vertex Cover. The Integral LP is formulated as follows (E is our set of edges, x the vertices):
Since Integral LP is also NP Hard, we can relax the integrality constraint to get a fractional LP:
Once we have a fractional solution, we round these off to get a 2 approximation. While this doesn't seem any better than the greedy approximation, it does have the advantage of working just as well for weighted edges (just multiply x_i by w_i in the objective function), while the greedy algorithm doesn't have a weighted analog.
The Metric Facility Location problem [notes][wiki] is the problem of trying to place "facilities" (think retail locations) in order to serve customers. Facility i costs f_i to build, and it costs customer j c_ij to travel to facility i. The "rounding" step of this relaxation is much more involved. Whereas in vertex cover we only had to consider the two end points of a given edge, here a facility may have many "clients". The basic intuition is to "filter" the expensive c_ij, then "cluster" the fractional facilities that are close to each other, open the min cost facility and drop the others, and reassign customers from the dropped facilities to the min cost facility. Because of the triangle inequality, we know that we haven't lost too much by doing this reassignment.
Key ideas:
The idea is that we create a new LP, call it LP' (LP prime), that has a trivially feasible solution. So we take our original LP and add a barrier function. This barrier function sums the logs of the slack variables, so as the slack variables become smaller (that is, we get closer to optimum), then our barrier function approaches infinity. We balance this out by introducing a parameter (Nelson uses lambda λ, Karger mu μ) that shifts the weight of the objective function from the barrier function to the original objective. So our LP' looks something like:
This is basically dipping our toes into convex optimization. When he explains Newton's method it's basically wall to wall calculus. At some point I got curious about James Renegar, who was mentioned as having improved the time bounds on interior point, and found this seminar he gave on first order methods (video). Again it was super heavy on the math...
Multiplicative weights is a simple algorithm at heart. The basic problem is that we have to make a stream of decisions (like, say, buying stock), and we want to minimize our regret. That is to say we want to make as few mistakes as possible. While we don't have access in information in the future (like in real life), we are often given a group of n "experts" making the same decision.
The naive algorithm is to just take a majority vote among these experts, but it turns out it isn't hard to produce a pathological case where you do worth than any expert by doing this (you get it wrong all the time, yay!)
We don't know a priori that A is going to be right 100% of the time, and none of the other experts do worse that 33% (though you can shift them around pretty arbitrarily, as long as it's a 3/4 split in this example). If we gradually give experts more weight when they make correct predictions, we will eventually start making correct guesses:
This survey paper covers several variations on MW: paper. It has plenty of links to other resources for a deeper dive. Moitra lecture 17 (MIT 2016) covers the topic as well. Nelson goes over the packing/covering LP approximation algorithm using MW by Plotkin etal in lecture 20. The "experts" in the LP solving version are the constraints, and there is an "oracle" involved... but honestly I didn't really follow it very well.
This unit covers Flow Networks, mostly max flow problems. William Fiset has a YouTube channel with some nice visualizations of several flow algorithms: Ford-Fulkerson, Capacity Scaling, Edmonds-Karp, Dinic's Algorithm. Also found this simulator at visualgo.net that runs FF, EK, or Dinic on a custom flow graph. Finally, this article on cp-algorithms.com walks through FF and EK step by step with pictures (the site has articles on plenty of other algos along with implementations written in c++). I think these visualizations are much better than anything I would whip up, so I won't bother =).
Karger, Lectures 9-12. Lecture 8 and Lecture 9 are review, mostly just terminology, axioms, and various flavors of augmenting path algorithms (e.g. Ford-Fulkerson), mostly stuff I covered in 6.046 (which would be more helpful if I actually remembered most of it...). Lecture 10 opens with a discussion of Edmonds-Karp, which works by find a shortest path from S to T and augmenting along that path first, yielding a O(E² * V)... alternatively O(m² * n) as Karger likes to use m for edges and n for vertices. He then covers Dinic's blocking flow algorithm.
In Lecture 11 Karger covers using link-cut trees to improve the performance of Dinic's algorithm. He also covers min-cost max flow, and min-cost circulation, and demonstrates how the two problems reduce to each other. The idea with min-cost flow is that we have edge costs and we are trying not only to maximize flow, but also minimize the cost of that flow. Edges can have negative costs (i.e. they are "profitable"), and it is natural to think about negative cost circulations in our graph that saturate these profitable edges as much as possible.
In Lecture 12 Karger covers a "reduced cost" algorithm for min cost flows, which provides a strongly polynomial algorithm for finding these flows. Found some interesting notes by Sleator on the CMU site: [notes]. This paper by Goldberg and Tarjan on min-cost circulations also seems relevant: [paper].
Nelson introduces the flow problem by giving an LP formulation for max flow (aaaahhh no more LP kill me now!). The basic constraints on the flow problem itself bear repeating since he uses them in the LP formulation. An s-t flow is a vector such that (E is set of edges):
Nelson mentions that one of the best bounds achieved for this formulation was Daitch and Speilman in 2008 [Faster Approximate Lossy Generalized Flow]. Their algorithm uses a standard interior point method approach, but exploits the properties of the intermediate LP's arising from network flows. Last third of lecture 20 Nelson says he isn't going to describe Ford-Fulkerson, then goes on to describe Ford-Fulkerson anyway lol. He made a point of stating the correctness theorem for FF: A flow f is a max flow if there is no augmenting path in the residual graph.
The best strongly polynomial algorithm for max flow is O(nm) flow algorithm by Orlin 2013 [download paper]. The best weakly polynomial bound is by Goldberg Rao, 1998 [paper] (it's a weird bound involving 2/3 and 1/2 exponents plus some log factors). King-Roa-Tarjan algorithm from 1994 [paper] with some weird bounds.
The capacity scaling algorithm [paper] hinges on a bit trick, where we operate on an alternative representation of the graph, G', in which we gradually shift in the bits from the original graph. We start with G' having all zero capacities. We then do a bit shift, bringing in the most significant bit of the capacities (assume leading zeros so each representation is the same size). We now have some capacities equal to 1. We run augmenting paths until we have a max flow in G', then we repeat, shifting the flow values and capacities one bit to the right (doubleing everything) and adding in the next most significant bit. This works efficiently because at each iteration, at most m capacity has been added to the min cut in G', so running augmenting paths is effectively tied to the combinatorics and not the capacity values.
Nelson also covers Dinic's algorithm. The cp-algorithms.com site includes a page on Dinic's which includes a c++ implementation. I'll list the highlights of Dinic's here:
Blocking flows gets a bound of O(m * √n) when used for bipartite matching. For general graphs, the runtime can be broken down as (iterations) x (time to find blocking flow), which works out to (n) * (mn) or O(n²m).
Lecture 23 covers heavy/light decomposition [wiki] as a tool for analyzing the runtim of link-cut trees (it is discussed in link-cut tree paper). Follows with min-cost max flow, reduction to and from min-cost circulation. He then goes over the "reduced price" algorithm is much the same way Karger did.
In lecture 9, Nelson describes a paging algorithm called "Mark". The algorithm is pretty straightforward:
Think of the algorithm as working over a series of "phases". At the beginning of a phase, all the items in the cache are unmarked. When items are put in the cache (or items still in the cache are accessed), they are "marked". When items are brought into the cache, they evict an unmarked item uniformly at random. This algorithm is 2H(k) competitive, that is 2 x (kth harmonic number). Harmonic numbers are approximated by the natural log, so if k = 8 billion (main memory vs disk example), then our algorithm is about 2 * 22.8 ≈ 46 competitive.
Jelani introduces the "Primal/Duel framework" for analyzing online algorithms. The way this works is that we define a linear program for the thing we want to minimize (money spent on ski's perhaps), and then use the property of weak duality to define upper and lower bounds on the competitive ratio based on the primal and duel solutions. Karger covers duality in lecture 15 of the MIT series, providing an interesting analogy to physics to color our intuition. He also shows how to get the duel for an arbitrary LP (vs a Standard Form LP). Karger works some examples in lecture 16.
[At this point I'm fully out of gas for taking notes, so don't expect in-depth analysis from here, rather mostly links to references and quick summaries. It doesn't help that much of the remainder of the class leans so heavily on LP which, sorry, I don't find terribly interesting...]
Approximation Algorithms (CS224, Lectures 11-12)
Some of the basic vocabulary for approximation algorithms was introduced in 6.046, so I'll keep it pretty brief here:
- PTAS - Polynomial Time Approximation Scheme
- FPTAS - Fullty Polynomial Time Approximation Scheme
- FPRAS - Fully Polytime Randomized Approximation Scheme
Knapsack has straightforward DP solutions that run in pseudo polynomial time. They aren't true poly solutions because they rely on the size of the input W, which is represented by lg(W) bits. Fortunately it does admit a FPTAS. First we look at some greedy algorithms.
The first approximation algorithm Jelani suggests is a greedy algorithm that sorts the items by value ratio and takes items till no more will fit. However, this naive algorithm can do quite terrible. Imagine we have two items with the following weights and values:
Item 1 has a slightly better value ratio and gets picked first, but then item 2 won't fit, so we get a W competitive algorithm, blech! We can improve this by taking modifying our algorithm so that we take either the output of greedy, OR the most valuable item, at every step. This gives us a 2 approximation.
A PTAS for Knapsack goes like this: First, consider two observations -
- If no item has value ε * OPT, then greedy achieves at least (1 - ε) * OPT
- At most 1/ε items in OPT solution can have value at least ε * OPT
So we select subset S, containing at most 1/ε items. These are the "big items". Remove any remaining items with value > anyone in S. Now run greedy on what is left over. We get an optimal approximation when we "guess" S correctly, so we just run this subroutine on all n^(1/ε) different subsets. Because epsilon is in the exponent of n, this is not an FPTAS. (the scribe notes were key to helping me understand what this algorithm was actually doing... "guess S, what??" lol).
In lecture 12, Nelson covers an FPTAS for Knapsack. This approach scales the problem so that running the O(nV) DP algorithm is efficient. Each item has it's value multiplied by n / (ε * v_max) where v_max is the highest value of any item in the set, and then is rounded down. We then calculate OPT' (opt prime) on this scaled problem. This doesn't give us an optimal value because each item lost at most 1 in value due to rounding. Karger also covers this algorithm in his course.
Some problems don't admit an FPTAS, such as bin packing. For bin packing, this is due to the fact that even the decision problem formulation (i.e. "can these items fit in x bins") is NP-Hard. So if we have a 1 - ε approximation (say, "this bin packing uses 2.2 bins") then we can round this to the integral solution and then P == NP.
Next look at DNF Counting. DNF is similar to SAT (which is in CNF format). There is a polynomial time algorithm for finding DNF assignments, however the problem of counting all the possible satisfying assignments is NP-Hard (actually it is in a complexity class call #P, which is even harder).(FPRAS) due to KLM [paper]. The basic intuition of this algorithm is sampling: we make a random assignment to the items in the DNF and check if it is a satisfying assignment. The problem is that there may be an exponentially small number of satisfying assignments, which means we need to take exponential number of samples to get a good estimate. The workaround involves creating a surrogate set representing the original that is more amenable to sampling (I'm not even going to try to explain it, I don't really get it). The poly-n bounds are proved using Chernoff.
Semi-definite programming (Vandenberghe and Boyd [paper]) is touched on briefly. SDP is used by Goemans and Williamson [paper] to get a much better competitive ratio in Max Cut approximation (0.878 vs 0.5). The problem is formulated as a quadratic program, relaxed to vector dot products, solved yielding a bunch of unit vectors, which are then partitioned with a random hyperplane. Moitra spends all of lecture 19 [6.854 SP16] covering SDP and the Goemans-Williamson algorithm in much more depth.
## CS224 Lecture 13 is a guest lecture on unsupervised machine learning.
Karger covers approximation algorithms in lectures 19-22 of the MIT sequence. The remainder of this section are notes I took on the Karger lectures:
Absolute approximation are within some additive value of OPT. Planar graph coloring is an example. Any planar graph has a four coloring, so we need at most 4 colors, which would be at worst a 3 absolute approximation (we need at least one color). If the graph has an edge, we need at least two colors, making the 4 coloring a 2 approximation. However, if the graph has an odd cycle, then we need at least three colors, in which case the 4 coloring is a 1 approximation. In the case of a graph with no odd cycles, it it bipartite and can be colored with 2 colors.
Absolute approximations almost never exist. Karger explains this using a scaling argument: when we can scale the problem by the additive factor and solve, we end up within k/(k + 1), which basically gives us OPT (I'm probably butchering the explanation but that's the gist of it). Most approximations are described as being within a multiplicative factor α, called a relative approximation.
Greedy 2-approximate algorithm for Max-cut [wiki]: As you place a vertex, place it on the side of the cut with the minority of its placed neighbors. The best OPT can achieve is m, the number of edges in a graph (that is, a cut that goes through every edge), and because at every step we are creating at least as many cut edges as uncut edges, our approximation is at least 0.5 OPT (i.e. 1/α, α = 2, therefore "2 approximate").
Greedy Set Cover approximation achieves a O(ln n) ratio: At each step, we take the set that covers the most uncovered items. Suppose OPT = k (i.e. OPT uses k sets to cover all vertices), then there must be a set that covers n/k vertices in the first step. In each successive step at least a (1 - 1/k) portion of the remaining vertices are covered. When this portion is < 1, then the algorithm terminates. The wiki page includes an example where the approximation algorithm chooses three sets, where OPT would choose 2.
Greedy vertex cover achieves a 2 approximation: find an uncovered edge, and take both endpoints. Because OPT contains all edges, we know that at every step we are taking at least one vertex that is in OPT [wiki].
The scheduling problem involves putting j jobs on n machines for processing. Graham's algorithm (not called a "greedy algorithm" because apparently we didn't know about greedy algorithms yet) [1969 paper] acts in a greedy way by placing the jobs, in order, on the least loaded machine. This version of the algorithm achieves (2 - 1/m) OPT for the max load, and has the advantage of maintaining this ration even when jobs are coming online. The "Longest Processing Time" rule improves the ratio to 4/3, but this requires that we know all the jobs ahead of time. [slides I found useful]
Karger describes an algorithm for the P||C_max problem (scheduling j jobs on m machines that run in parallel, minimizing the max completion time). It is almost identical to the Knapsack approximation scheme.
Covers approximation of TSP. The naive MST approximation gets a 2 competitive ratio, but he also covers Christofides algorithm, which improves upon the MST based approximation by using a better rounding scheme. Instead of doubling up every edge (which yields the 2 approximation), it converts the MST into an Euler graph by matching up the odd degree vertices. This creates an Euler tour. Since we know that the MST is ≤ OPT, and a min-cost perfect bipartite matching of the odd vertices is ≤ OPT / 2, we get a 3/2 OPT approximation. Also mentions the Held-Karp bound [paper], but doesn't go into it.
Karger covers the LP relaxation of Vertex Cover. The Integral LP is formulated as follows (E is our set of edges, x the vertices):
- min Σx_i
- x_i + x_j ≥ 1 ∀ (i, j) ∈ E
- x_i = 1 if in cover, 0 otherwise
Since Integral LP is also NP Hard, we can relax the integrality constraint to get a fractional LP:
- min Σx_i
- x_i + x_j ≥ 1 ∀ (i, j) ∈ E
- 0 ≤ x_i ≤ 1
Once we have a fractional solution, we round these off to get a 2 approximation. While this doesn't seem any better than the greedy approximation, it does have the advantage of working just as well for weighted edges (just multiply x_i by w_i in the objective function), while the greedy algorithm doesn't have a weighted analog.
The Metric Facility Location problem [notes][wiki] is the problem of trying to place "facilities" (think retail locations) in order to serve customers. Facility i costs f_i to build, and it costs customer j c_ij to travel to facility i. The "rounding" step of this relaxation is much more involved. Whereas in vertex cover we only had to consider the two end points of a given edge, here a facility may have many "clients". The basic intuition is to "filter" the expensive c_ij, then "cluster" the fractional facilities that are close to each other, open the min cost facility and drop the others, and reassign customers from the dropped facilities to the min cost facility. Because of the triangle inequality, we know that we haven't lost too much by doing this reassignment.
Linear Programming (CS224, Lecture 15-18)
Lecture 15 is spent reviewing Standard Form, complementary slackness, and Simplex. It's a good refresher but I didn't take much in the way of notes because I already covered it in 6.046. I think the one nugget for basics was the impact of the pivoting rule in Simplex. A naive pivoting rule can lead to cycles (causing Simplex to stop making progress), however we learned how Bland's Rule can avoid these cycles.
Karger covers LP in MIT lectures 13-18. Early on he mentions "disrupting Soviet railway networks" as a motivation for LP, I found a relevant paper here. 13 and 14 cover the basics, 15 and 16 duality, 17 Simplex, and 18 interior point. I like Karger's teaching style and I think these were worth watching, but I didn't take many notes on 13-14 and 17 for the same reason as above. Duality I covered above, and I did take some notes on ellipsoid and interior point.
Karger covers LP in MIT lectures 13-18. Early on he mentions "disrupting Soviet railway networks" as a motivation for LP, I found a relevant paper here. 13 and 14 cover the basics, 15 and 16 duality, 17 Simplex, and 18 interior point. I like Karger's teaching style and I think these were worth watching, but I didn't take many notes on 13-14 and 17 for the same reason as above. Duality I covered above, and I did take some notes on ellipsoid and interior point.
Nelson touches on ellipsoid briefly (like, <15 minutes) toward the end of lecture 16. Karger spends roughly the same amount of time on it (end of MIT lecture 17). The intuition is that we "surround" the polytope of our target LP with an ellipsoid, and check the center for feasibility. We do this check by consulting an "oracle" that will give us a separating hyper plane for any violated constraint. If we don't have a feasible point, we translate the hyper plane to the center of our ellipsoid, creating two halves. We then squash and stretch our ellipsoid so that is still covers the half containing our polytope. We do this till we either get a feasible point, or until our ellipsoid is "too small" from a precision standpoint.
Because an optimum solution may have 0 volume (i.e. it's a single point), we need to loosen the constraints on our original LP by a tiny fraction. This creates a tiny volume that can be found by the algorithm. While ellipsoid is not used in practice (for LPs anyway) because it's too slow (the polynomial is about n^6), it does have this interesting property that you don't even need to be able to write down the LP you are optimizing, you just need the separation oracle to give you a violated constraint. I also found some scribe notes from the Princeton equivalent of this class that includes some nice visuals.
Because an optimum solution may have 0 volume (i.e. it's a single point), we need to loosen the constraints on our original LP by a tiny fraction. This creates a tiny volume that can be found by the algorithm. While ellipsoid is not used in practice (for LPs anyway) because it's too slow (the polynomial is about n^6), it does have this interesting property that you don't even need to be able to write down the LP you are optimizing, you just need the separation oracle to give you a violated constraint. I also found some scribe notes from the Princeton equivalent of this class that includes some nice visuals.
Path following interior point (Karmarkar's algorithm) [paper] is covered by Nelson in lectures 17-18, and Karger in MIT lecture 18. Where ellipsoid has an "outside-in" kind of intuition, encircling the whole polytope and then slowing shrinking in on it, interior point has sort of the opposite intuition, where we want to push a point as far inside the feasible region that we can, and then gradually creep out toward the boundary of the polytope.
Key ideas:
- barrier function
- gradient decent to stay on the "central path"
- analytic center
The idea is that we create a new LP, call it LP' (LP prime), that has a trivially feasible solution. So we take our original LP and add a barrier function. This barrier function sums the logs of the slack variables, so as the slack variables become smaller (that is, we get closer to optimum), then our barrier function approaches infinity. We balance this out by introducing a parameter (Nelson uses lambda λ, Karger mu μ) that shifts the weight of the objective function from the barrier function to the original objective. So our LP' looks something like:
- MIN λcx + p(s(x)) where p(x) = -Σ log(s(x)_i)[Nelson]
- MIN cx - μΣ ln(x_i) [Karger]
- (basically identical)
In Nelson's version you would start with λ "exponentially small in the inputs", which makes the cx portion of the LP negligible. Starting from a feasible solution to this, we gradually increase the value of λ until we have a solution that we can "round off" to an optimal solution to the original LP. Karger is the same basic idea, except instead of adding more weight to the original objective he gradually takes weight away from the barrier. Tomato tomawto.
Starting from the "analytic center" of LP', we follow the "central path"... a multidimentional curve, through the interior of the polytope. Karger explains this as essentially taking a tangent, moving a little ways along that tangent to make some progress, then using gradient descent to get back onto the central path.
Nelson covers Newton's Method (Second Order method) in addition to gradient descent. The one thing I remembered from this is that we iterate on the kth step until we get a 1/100 (fine) approximator, which we can then use as a course (1/3) approximation for the kth + 1 step. We then iterate on this new function until it's fine again, rinse repeat. They both go through the math, which there is no point in me trying to awkwardly replicate here. Nelson is much heavier on the math than Karger; I had to keep stopping to look stuff up:
- What's a Hessian matrix? (basically a second derivative)[Khan Acad.]
- Review eigenvalues/vectors [link]
- What is a projection? [link]
- What is the minus two power of a matrix? [link]
- What is an L2 and L1 norm? Infinity norm?? whaaaaat? [link]
This is basically dipping our toes into convex optimization. When he explains Newton's method it's basically wall to wall calculus. At some point I got curious about James Renegar, who was mentioned as having improved the time bounds on interior point, and found this seminar he gave on first order methods (video). Again it was super heavy on the math...
Multiplicative Weights (CS224, Lecture 19-20)
Multiplicative weights is a simple algorithm at heart. The basic problem is that we have to make a stream of decisions (like, say, buying stock), and we want to minimize our regret. That is to say we want to make as few mistakes as possible. While we don't have access in information in the future (like in real life), we are often given a group of n "experts" making the same decision.
The naive algorithm is to just take a majority vote among these experts, but it turns out it isn't hard to produce a pathological case where you do worth than any expert by doing this (you get it wrong all the time, yay!)
We don't know a priori that A is going to be right 100% of the time, and none of the other experts do worse that 33% (though you can shift them around pretty arbitrarily, as long as it's a 3/4 split in this example). If we gradually give experts more weight when they make correct predictions, we will eventually start making correct guesses:
This survey paper covers several variations on MW: paper. It has plenty of links to other resources for a deeper dive. Moitra lecture 17 (MIT 2016) covers the topic as well. Nelson goes over the packing/covering LP approximation algorithm using MW by Plotkin etal in lecture 20. The "experts" in the LP solving version are the constraints, and there is an "oracle" involved... but honestly I didn't really follow it very well.
Network Flows (CS224, Lecture 20-23)
This unit covers Flow Networks, mostly max flow problems. William Fiset has a YouTube channel with some nice visualizations of several flow algorithms: Ford-Fulkerson, Capacity Scaling, Edmonds-Karp, Dinic's Algorithm. Also found this simulator at visualgo.net that runs FF, EK, or Dinic on a custom flow graph. Finally, this article on cp-algorithms.com walks through FF and EK step by step with pictures (the site has articles on plenty of other algos along with implementations written in c++). I think these visualizations are much better than anything I would whip up, so I won't bother =).
Karger, Lectures 9-12. Lecture 8 and Lecture 9 are review, mostly just terminology, axioms, and various flavors of augmenting path algorithms (e.g. Ford-Fulkerson), mostly stuff I covered in 6.046 (which would be more helpful if I actually remembered most of it...). Lecture 10 opens with a discussion of Edmonds-Karp, which works by find a shortest path from S to T and augmenting along that path first, yielding a O(E² * V)... alternatively O(m² * n) as Karger likes to use m for edges and n for vertices. He then covers Dinic's blocking flow algorithm.
In Lecture 11 Karger covers using link-cut trees to improve the performance of Dinic's algorithm. He also covers min-cost max flow, and min-cost circulation, and demonstrates how the two problems reduce to each other. The idea with min-cost flow is that we have edge costs and we are trying not only to maximize flow, but also minimize the cost of that flow. Edges can have negative costs (i.e. they are "profitable"), and it is natural to think about negative cost circulations in our graph that saturate these profitable edges as much as possible.
In Lecture 12 Karger covers a "reduced cost" algorithm for min cost flows, which provides a strongly polynomial algorithm for finding these flows. Found some interesting notes by Sleator on the CMU site: [notes]. This paper by Goldberg and Tarjan on min-cost circulations also seems relevant: [paper].
Nelson introduces the flow problem by giving an LP formulation for max flow (aaaahhh no more LP kill me now!). The basic constraints on the flow problem itself bear repeating since he uses them in the LP formulation. An s-t flow is a vector such that (E is set of edges):
- flow is non-negative (f ≥ 0)
- flow is conserved at intermediate nodes, i.e. ∀ v ∉ {s, t}, flow in v == flow out v
- flow out s == flow in t
- feasibility: ∀ e ∈ E, flow(e) ≤ capacity(e)
LP form:
MAX [e = (s, u)∈ E] Σ flow(e) // maximize flow out of s
non-negativity: f ≥ 0
constraints for (2): Σ f(u → v) == Σ f(v → w)
constraint for (3): Σ f(s → u) == Σ f(v → t)
feasibility constraints for (4): f(e) ≤ c(e)
Nelson mentions that one of the best bounds achieved for this formulation was Daitch and Speilman in 2008 [Faster Approximate Lossy Generalized Flow]. Their algorithm uses a standard interior point method approach, but exploits the properties of the intermediate LP's arising from network flows. Last third of lecture 20 Nelson says he isn't going to describe Ford-Fulkerson, then goes on to describe Ford-Fulkerson anyway lol. He made a point of stating the correctness theorem for FF: A flow f is a max flow if there is no augmenting path in the residual graph.
The best strongly polynomial algorithm for max flow is O(nm) flow algorithm by Orlin 2013 [download paper]. The best weakly polynomial bound is by Goldberg Rao, 1998 [paper] (it's a weird bound involving 2/3 and 1/2 exponents plus some log factors). King-Roa-Tarjan algorithm from 1994 [paper] with some weird bounds.
The capacity scaling algorithm [paper] hinges on a bit trick, where we operate on an alternative representation of the graph, G', in which we gradually shift in the bits from the original graph. We start with G' having all zero capacities. We then do a bit shift, bringing in the most significant bit of the capacities (assume leading zeros so each representation is the same size). We now have some capacities equal to 1. We run augmenting paths until we have a max flow in G', then we repeat, shifting the flow values and capacities one bit to the right (doubleing everything) and adding in the next most significant bit. This works efficiently because at each iteration, at most m capacity has been added to the min cut in G', so running augmenting paths is effectively tied to the combinatorics and not the capacity values.
Nelson also covers Dinic's algorithm. The cp-algorithms.com site includes a page on Dinic's which includes a c++ implementation. I'll list the highlights of Dinic's here:
- Construct a "level graph", which is a subset of edges that strictly make progress toward t.
- Create a blocking flow by pushing flow along augmenting paths in the level graph
- running time for creating a blocking flow is O(nm), since in each iteration we delete at least one edge because it is either a dead end, or it was saturated by an augmenting path
- Add the blocking flow to our flow f, recreate level graph, repeat up to n iterations. We know this is n because each iteration pushes out the shortest path at least one, and once the shortest path is equal to the number of vertices in the graph, we are done.
Blocking flows gets a bound of O(m * √n) when used for bipartite matching. For general graphs, the runtime can be broken down as (iterations) x (time to find blocking flow), which works out to (n) * (mn) or O(n²m).
Nelson goes much deeper into the details on using link-cut trees to speed up blocking flows [paper][wiki]. Link-cut trees improve this bound by reducing the time to find a blocking flow to O(m log n). They do this by allowing us to "reuse" information we gain about partial paths to t in the level graph. When we are searching for an augmenting path, we basically get to "skip forward" through the level graph so we aren't spending as much time retracing the same edges. The link-cut trees are based on splay-trees. Lecture 22 is mostly Nelson walking through the pseudo-code for link cut trees.
Lecture 23 covers heavy/light decomposition [wiki] as a tool for analyzing the runtim of link-cut trees (it is discussed in link-cut tree paper). Follows with min-cost max flow, reduction to and from min-cost circulation. He then goes over the "reduced price" algorithm is much the same way Karger did.
Faster Exponential Algorithms (CS224, Lectures 24-25)
This unit covers a few algorithms for finding solutions to NP-Hard problems exactly with "faster" exponential algorithms. Following the white rabbit in the notes, I found the site of Jeff Erickson at University of Illinois - Urbana, which includes a section on NP-Hard problems that is quite robust.
The first is an "exponential divide and conquer" algorithm for the Traveling Salesman Problem. The brute force algorithm basically looks at every permutations of the path in the graph and finds the lowest distance tour, giving a time complexity of O(n!) and poly-n space. Dynamic programming can get time and space bounds of O(2^n) by trading off for time for space.
The Divide and Conquer algorithm for TSP works by picking a point m, and breaking the tour down by looking at the best tour that goes through half the points and ends at m, and the remaining half of the points out of m. In other words, OPT(U, s, t) = OPT(S, s, m) + OPT(T, m, t). The base case is when there are only two points (only one path from a to b). This recurrance works out to something like O(4^n + poly-n).
Another approach is pruned brute force, using 3SAT as an example problem this time. The brute force algorithm for 3SAT is O(2^n) with poly space. Another way to approach this is to look at each of the three variables in a clause, x, y, and z, and do the following:
Notation: φ | x is the formula obtained by setting the variable x to true
if SAT(φ | x) return true
elif SAT(φ | y !x) return true
elif SAT(φ | z !y !x) return true
else return false
In the base algorithm, we end up with an O(3^n) bound, worse than the straight forward brute force. However, we can use the fact that if we fall through the first if clause, we were not able to find a satisfying assignment with x set to true, so we just assume x is set to false. When we get to the third predicate, we can set x and y both to false. This gives us a recursion of T(n) = T(n - 1) + T(n - 2) + T(n - 3), which gives us a bound of O(~1.84^n).
Another algorithm for 3SAT is to start with an assignment (say, all ones or all zeros). While there exists an unsatisfied clause, flip each variable in that clause and recurse at most n/2 depth. The reason for the n/2 limit is that the hamming distance between a satisfying assignment and our assignment is at most n/2 (if we take an assignment and it's negation to be equivalent). Runtime is O(√3^n) or about O(~1.73^n).
Schöning algorithm [paper] gets time of O(~1.33^n) using randomization, and it is super simple:
Assign the variables uniformly at random.
Repeat up to 3n time:
pick the first unsatisfied clause
flip one of the variables in that clause uniformly at random
That is all that involved for one iteration. The key to getting a high probability bound is that we have to repeat this procedure exponentially many times. Nelson illustrates this with Markov chains. Before moving on to the last thing, he mentions that DPLL is still commonly used and is fast in practice.
Toward the end of lecture 24 Nelson quickly goes over k-coloring using inclusion/exclusion [paper1][paper3]. The brute force algorithm for k-coloring takes O(k^n), and DP takes O(3^n) time and O(2^n) space. However with inclusion/exclusion, we can either improve the DP space complexity to poly-n, or improve time to O(2^n). This involves using a function called a "fast zeta transform" and computing it for every subset of S [zeta transform paper]. I'm not sure what, if any, relation this has to the z transform from signals processing [z-transform video]... (probably none, but I can't be sure...). There is also something about a Mobius transform in there... he goes through it pretty fast and I kind of lost the plot...The first is an "exponential divide and conquer" algorithm for the Traveling Salesman Problem. The brute force algorithm basically looks at every permutations of the path in the graph and finds the lowest distance tour, giving a time complexity of O(n!) and poly-n space. Dynamic programming can get time and space bounds of O(2^n) by trading off for time for space.
The Divide and Conquer algorithm for TSP works by picking a point m, and breaking the tour down by looking at the best tour that goes through half the points and ends at m, and the remaining half of the points out of m. In other words, OPT(U, s, t) = OPT(S, s, m) + OPT(T, m, t). The base case is when there are only two points (only one path from a to b). This recurrance works out to something like O(4^n + poly-n).
Another approach is pruned brute force, using 3SAT as an example problem this time. The brute force algorithm for 3SAT is O(2^n) with poly space. Another way to approach this is to look at each of the three variables in a clause, x, y, and z, and do the following:
Notation: φ | x is the formula obtained by setting the variable x to true
if SAT(φ | x) return true
elif SAT(φ | y !x) return true
elif SAT(φ | z !y !x) return true
else return false
In the base algorithm, we end up with an O(3^n) bound, worse than the straight forward brute force. However, we can use the fact that if we fall through the first if clause, we were not able to find a satisfying assignment with x set to true, so we just assume x is set to false. When we get to the third predicate, we can set x and y both to false. This gives us a recursion of T(n) = T(n - 1) + T(n - 2) + T(n - 3), which gives us a bound of O(~1.84^n).
Another algorithm for 3SAT is to start with an assignment (say, all ones or all zeros). While there exists an unsatisfied clause, flip each variable in that clause and recurse at most n/2 depth. The reason for the n/2 limit is that the hamming distance between a satisfying assignment and our assignment is at most n/2 (if we take an assignment and it's negation to be equivalent). Runtime is O(√3^n) or about O(~1.73^n).
Schöning algorithm [paper] gets time of O(~1.33^n) using randomization, and it is super simple:
Assign the variables uniformly at random.
Repeat up to 3n time:
pick the first unsatisfied clause
flip one of the variables in that clause uniformly at random
That is all that involved for one iteration. The key to getting a high probability bound is that we have to repeat this procedure exponentially many times. Nelson illustrates this with Markov chains. Before moving on to the last thing, he mentions that DPLL is still commonly used and is fast in practice.
Before moving on to streaming he describes Yates algorithm, which is a DP formulation of inclusion/exclusion. And that's it for "fast" exponential algorithms.
Plugs "Algorithms for Big Data" and then goes on to describe the basic motivation of streaming algorithms. Consider if we have some high-dimensional vector representing requests in a router, where n is all IPv6 addresses and m is our stream of requests. We want to be able to answer queries about this vector, such as the number of unique IP addresses that our router has seen. Naively, we can either save all the IP addresses, or save all the requests, but either of these gives us pretty crappy space bounds. Nelson proves that, unfortunately, it is impossible to use less than this space in a deterministic algorithm. He notes that it is also impossible to have a deterministic approximation algorithm, or a randomized exact algorithm, for basically the same reason (has to do with encoding and the pidgeon hole principle). However, a randomized approximation algorithm called Flajolet-Martin is feasible [paper].
The way this algorithm works is that you maintain a vector, z, of length R, and also R different hash functions that map an item to the interval (0, 1). For each item i in our stream, compute MIN(z, h(i)) for each hash function. Think of it as computing R random numbers from 1 to R, and keeping the min of what we have seen for each of them. To answer the query for how many items we've seen, return 1/AVG(z) - 1. This is simple enough you can actually do it (crudely) in a spreadsheet:
Here I have R=48, and I still get pretty crappy approximations at times, however even if I had a million requests, I would only have to store the 48 z values and hash functions. This would be a fun coding exercise, I really don't think it's a good idea extending this spreadsheet though, since it is basically calculating ~10k random numbers every time the page updates, yeesh. In order to get an error rate of 1%, I would need 10,000 hash functions (R = 1 / ε²), which falls out of Chebyshev's inequality.
Last lecture covers "Power of random signs", which is useful for things such as:
Streaming/Sketching (CS224, Lectures 25-26)
Plugs "Algorithms for Big Data" and then goes on to describe the basic motivation of streaming algorithms. Consider if we have some high-dimensional vector representing requests in a router, where n is all IPv6 addresses and m is our stream of requests. We want to be able to answer queries about this vector, such as the number of unique IP addresses that our router has seen. Naively, we can either save all the IP addresses, or save all the requests, but either of these gives us pretty crappy space bounds. Nelson proves that, unfortunately, it is impossible to use less than this space in a deterministic algorithm. He notes that it is also impossible to have a deterministic approximation algorithm, or a randomized exact algorithm, for basically the same reason (has to do with encoding and the pidgeon hole principle). However, a randomized approximation algorithm called Flajolet-Martin is feasible [paper].
The way this algorithm works is that you maintain a vector, z, of length R, and also R different hash functions that map an item to the interval (0, 1). For each item i in our stream, compute MIN(z, h(i)) for each hash function. Think of it as computing R random numbers from 1 to R, and keeping the min of what we have seen for each of them. To answer the query for how many items we've seen, return 1/AVG(z) - 1. This is simple enough you can actually do it (crudely) in a spreadsheet:
Here I have R=48, and I still get pretty crappy approximations at times, however even if I had a million requests, I would only have to store the 48 z values and hash functions. This would be a fun coding exercise, I really don't think it's a good idea extending this spreadsheet though, since it is basically calculating ~10k random numbers every time the page updates, yeesh. In order to get an error rate of 1%, I would need 10,000 hash functions (R = 1 / ε²), which falls out of Chebyshev's inequality.
Last lecture covers "Power of random signs", which is useful for things such as:
- L2 norm estimation [AMS99]
- Fast regression
- Point Query
- Dimensionality reduction
I think he spends most of the lecture going over linear sketching. The sense I got from it was that was sort of analogous to the idea from FM. I could probably come back later and get more out of this last lecture, or maybe check out Jelani's Algorithms for Big Data class, but I'm thoroughly tapped out on Advanced Algorithms.
[Ferris Bueller, in his pajamas]: "You're still here? It's over. Go home."

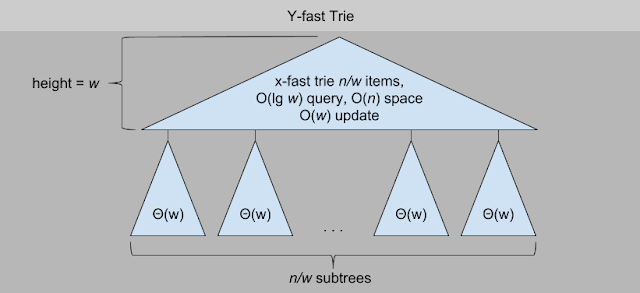











great summary and illustrations, thanks for sharing!
ReplyDeleteGood good good !. I watched MIT series too and here we have other people in the class. :)
ReplyDelete