Computational Objects
A perfect type of example for object based programming is electrical systems. All the connections between various electrical objects is "described" by wires. Digital circuits are a very abstract kind of electrical object.
Primitives and means of combination in digital circuits
(DEFINE A (MAKE-WIRE))
(DEFINE B (MAKE-WIRE))
(DEFINE C (MAKE-WIRE))
(DEFINE D (MAKE-WIRE))
(DEFINE E (MAKE-WIRE))
(DEFINE S (MAKE-WIRE))
(OR-GATE A B D)
(AND-GATE A B C)
(INVERTER C E)
(AND-GATE D E S)
wires carry abstract signals, can be voltage or even water pressure.
Going to build up an embedded language in LISP
(DEFINE (HALF-ADDER A B S C)
(LET ((D (MAKE-WIRE)) (E (MAKE-WIRE)))
(OR-GATE A B D)
(AND-GATE A B C)
(INVERTER C E)
(AND-GATE D E S)
We are using LISP lambda expressions as the glue.
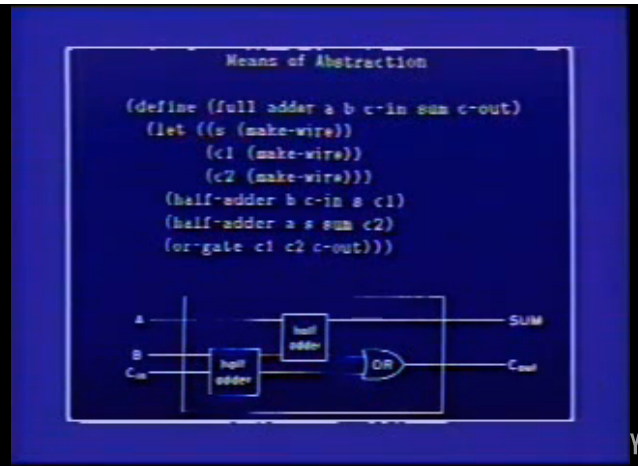
(DEFINE (FULL-ADDER A B C-IN SUM C-OUT)
(LET ((S (MAKE-WIRE))
(C1 (MAKE-WIRE))
(C2 (MAKE-WIRE)))
(HALF-ADDER B C-IN S C1)
(HALF-ADDER A S SUM C2)
(OR-GATE C1 C2 C-OUT)))
With these adders we can make adder-chains and big adders. This looks a little like the concepts behind the red stone computers I was seeing on youtube...
(DEFINE (INVERTER IN OUT)
(DEFINE (INVERTER-IN)
(LET ((NEW
(LOGICAL-NOT (GET-SIGNAL IN))))
(AFTER-DELAY INVERTER-DELAY
(LAMBDA ()
(SET SIGNALE! OUT NEW)))))
(ADD-ACTION! IN INVERTER-IN))
(DEFINE (LOGICAL-NOT S)
(COND ((= S 0) 1)
((= S 1) 0)
(ELSE
(PRINT "INVALID SIGNAL" S))))
and gates:
(DEFINE (AND-GATE A1 A2 OUTPUT)
(DEFINE (AND-ACTIO-PROCEDURE)
(LET ((NEW-VALUE
(LOGICAL-AND (GET-SIGNAL A1)
(GET-SIGNAL A2))))
(AFTER-DELAY AND-GATE-DELAY
(LAMBDA ()
(SET-SIGNAL! OUTPUT
NEW-VALUE)))))
(ADD-ACTION! A1 AND-ACTION-PROCEDURE)
(ADD-ACTION! A2 AND-ACTION-PROCEDURE))
We look at a simple circuit consisting of an and-gate and an inverter.
We assign an object and a relationship in the computer for every corresponding object in the world:
We have signals A and B which are connected by the and-gate action procedure. The output will interact with wire object C, which will connect to the inverter action procedure. Finally, this connects to another wire called D. Each wire will have a "signal". There must be an environment that binds signal (must be either 1 or 0). We also need a list of objects to inform if the signal changes, call it action procedures (AP). Also need input and output on the and-gate and inverter.
(DEFINE MAKE-WIRE
(LET ((SIGNAL 0) (ACTION-PROCS '()))
(DEFINE (SET-MY-SIGNAL! NEW)
(COND ((=SIGNAL NEW) 'DONE)
(ELSE
(SET! SIGNAL NEW)
(CALL-EACH ACTION-PROC))))
(DEFINE (ACCEPT-ACTION-PROC PROC)
(SET! ACTION-PROCS
(CONS PROC ACTION-PROCS))
(PROCS))
(DEFINE (DISPACTCH M)
(COND ((EQ? M 'GET-SIGNAL) SIGNAL)
((EQ? M 'SET-SIGNAL!)
SET-MY-SIGNAL!)
((EQ? M 'ADD-ACTION!)
ACCEPT-ACTION-PROC)
(ELSE
(ERROR "Bad Message" m))))
DISPATCH))
This program defines a wire. The CALL-EACH procedure is just CDRing down a list:
(DEFINE (CALL-EACH PROCEDURE)
(COND ((NULL? PROCEDURES) 'DONE)
(ELSE
((CAR PROCEDURES))
(CALL-EACH (CDR PROCEDURES)))))
(DEFINE (GET-SIGNAL WIRE)
(WIRE 'GET-SIGNAL))
(DEFINE (SET-SIGNAL! WIRE NEW-VALUE)
((WIRE 'SET-SIGNAL!) NEW-VALUE))
(DEFINE (ADD-ACTION! WIRE ACTION-PROC)
((WIRE 'ADD-ACTION!) ACTION-PROC))
(DEFINE (AFTER-DELAY DELAY ACTION)
(ADD-TO-AGENDA!
(+ DELAY (CURRENT-TIME THE-AGENDA))
ACTION
THE-AGENDA))
(DEFINE (PROPAGATE)
(COND ((EMPTY-AGENDA? THE-AGENDA)
'DONE)
(ELSE
((FIRST-TIME THE-AGENDA))
(REMOVE-FIRST-ITEM! THE-AGENDA)
(PROPAGATE))))
Apparently this simulator for digital circuits was used to design a computer (just a more complex version)
We're going to look at the "agenda" or "priority queue"
Agenda primitives:
(MAKE-AGENDA) -> produce new agenda
(CURRENT-TIME agenda) -> number representing time
(EMPTY-AGENDA? agenda) -> bool
(ADD-TO-AGENDA! time action agenda) -> inserts a procedure into an agenda at the appropriate time
(FIRST-ITEM agenda) -> gives us an action
(REMOVE-FIRST-ITEM agenda) -> self explanitory
Agenda is going to be a list, organized by time in sorted order. Things that happen at the same time are grouped.
[ | ]--->[ | ]----------->[ |/]
| | |
header [time|queue] [time|queue]
| | | |
10 | 30 |
| |
{list of things to do} {list of things to do}
If we want to insert a new time (say, 20) we have to change the CDR of the preceding time (time 10) and we have to set the CDR of the inserted item to the succeeding time (time 30). We have a header cell in case we want to insert a cell (say time 5) before the first item.
Queue is similar to an agenda
(MAKE-QUEUE) -> new queue
(INSERT-QUEUE! item queue)
(FRONT-QUEUE queue)
(EMPTY-QUEUE? queue)
[front pointer|rear pointer]
| |
[ | ]-------->[ |/]
| |
1 2
We have a rear pointer so we can add to the end without cycling through the whole queue. Resetting the front pointer allows us to easily delete the first queue item. The CDR of each queue item points to the next item in the queue
The axioms used to define CONS, CAR, and CDR don't tell the whole story, because they say nothing about IDENTITY.
(DEFINE A (CONS 1 2)) -> in some environment, we've defined a to consist of pointers to values 1 and 2)
a -> [ | ]
/ \
1 2
(DEFINE B (CONS A A))
b -> [ | ]
| |
a -> [ | ]
/ \
1 2
This creates a situation where B is an alias of A, so if we run
(SET! (CAR B) 3) we will get this:
(CAR A) -> 3
This really seems to follow the same logic as object references. If you have multiple pointers to the same reference value, if you change the underlying value then all the pointers to that data will return the new value.
(DEFINE (CONS X Y)
(LAMBDA (M) (M X Y))) - Alonzo Church came up with this
(DEFINE (CAR X)
(X (LAMBDA (A D) A)))
(DEFINE (CDR X)
(X (LAMBDA (A D) D)))
(CAR (CONS 35 47))
(CAR (LAMBDA (M) (M 35 47)))
((LAMBDA (M) (M 35 47)) (LAMBDA (A D) A))
((LAMBDA (A D) A) 35 47)
35
Now we are going to do something nasty to Alonzo. We modify his version to include permissions to set x and y:
(DEFINE (CONS X Y)
(LAMBDA (M)
(M X
Y
(LAMBDA (N) (SET! X N))
(LAMBDA (N) (SET! Y N)))))
(DEFINE (CAR X)
(X (LAMBDA (A D SA SD) A)))
(DEFINE (CDR X)
(X (LAMBDA (A D SA SD) D)))
(DEFINE (SET-CAR! X Y)
(X (LAMBDA (A D SA SD) (SA Y))))
(DEFINE (SET-CDR! X Y)
(X (LAMBDA (A D SA SD) (SD Y))))
Mr. Mullet (apparently the guy's name is David) couldn't follow the whole permissions business, and to be fair I didn't really follow it at first either. It almost seems a bit like we are defining a method for CAR and CDR for assignment. I wonder what the implications are for something like (SET! (CAR A) 3) with this new "permission" set up...


No comments:
Post a Comment